三角函数是数学中的重要组成部分，广泛应用于各个领域，在实际问题求解过程中，经常需要对三角函数进行求值，掌握高效求解三角函数值的方法具有重要意义，本文将介绍几种常用的三角函数求值高效解法，包括角度转换、公式变换、近似计算法等。

角度转换法

角度转换法是一种常用的三角函数求值方法，对于一些特殊角度，我们可以利用角度转换公式将其转换为熟悉的锐角或已知角度，从而快速求解三角函数值，对于角度为π/7或π/9等，我们可以尝试将其转换为其他已知角度的线性组合，进而利用三角函数的加减公式求解。

公式变换法

公式变换法是基于三角函数的恒等变换公式进行求解的方法，通过对三角函数公式进行变换，可以将复杂的三角函数表达式转化为简单的形式，从而方便求解，利用正弦、余弦、正切的相互转化公式，以及倍角公式、半角公式等，可以实现对三角函数的高效求值，在实际应用中，熟练掌握这些公式并灵活应用，可以大大提高求解效率。

近似计算法

近似计算法是一种基于数值分析方法的三角函数求值方法，对于一些难以直接求解的三角函数值，我们可以采用近似计算法得到其近似值，常用的近似计算法包括泰勒级数展开法、幂级数展开法等，这些方法具有收敛速度快、计算量小的优点，适用于求解复杂三角函数表达式或特定角度的三角函数值。

计算器与软件应用

随着科技的发展，现代计算器和计算机软件已经具备了强大的计算能力，在求解三角函数值时，我们可以充分利用这些工具进行计算，许多计算器软件都内置了丰富的三角函数求解功能，只需输入相应的角度或数值，即可快速得到结果，一些专业的数学软件还提供了符号计算功能，可以方便地求解复杂的三角函数表达式。

实例分析

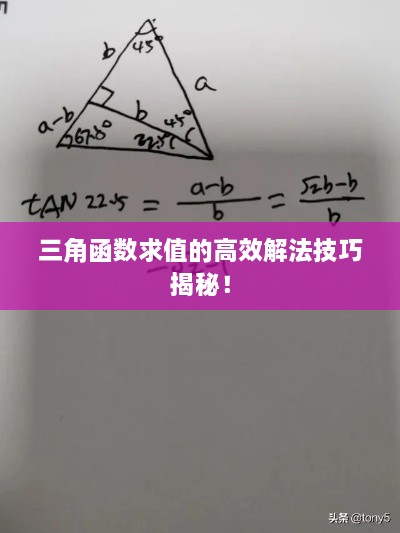
为了更好地说明三角函数求值高效解法的应用，本文给出几个实例进行分析，通过实例演示，展示角度转换法、公式变换法以及近似计算法在求解过程中的具体应用。

掌握高效的三角函数求值解法对于解决实际问题具有重要意义，本文介绍了角度转换法、公式变换法、近似计算法以及计算器与软件应用等方法，并给出了实例分析，在实际应用中，应根据问题的特点选择合适的方法进行计算，还需要不断学习和掌握新的求解技巧，以提高求解效率和准确性。

展望

随着数学理论的发展和计算机技术的进步，三角函数求值解法将会更加丰富和高效，未来研究方向包括：探索新的高效求解方法；研究三角函数的数值稳定性问题；开发更加智能的计算工具和软件，以更好地满足实际需求。